Woodworking
Last Updated Monday August 15, 2022
One of my favourite hobbies is woodworking. I think I always wanted to build stuff, and my Dad had some tools that I could use. Once I moved away from home I hardly had any tools at all. When I finally got a house of my own I started buying tools and making things with them. I made a few bookshelves and a small cabinet so David could store his thousands of diskettes and CDs. My workshop has been used as much for repairing broken stuff as it has for making new things, but I do dream of filling my house with furniture I made myself.
Some projects I have made
| Keepsake boxes | Pepper mills and salt shaker | Floppy Disk Drawers (1) (2) |
| Drill press stand | Workbenches | Saw horses |
| Book shelves | Desktop book shelves | Utility shelves |
| Panel cutter | Circle cutting jig | Box joint jig |
| Tool cabinet | Power sharpener | Router edge guide |
| Firewood stand | 14.5' x 8' Shed | Utility Trailer (1) (2) |
| Picnic table and benches | Window Sill Shelves | Router Table |
| Knife Holders | Mailbox | Off-cut Bin (1) (2) |
| Harry Potter Wand | Model Door | Pizza Peel |
| Ball In Cube | 4x4x4 Polycube Puzzle (1) (2) | Charcoal Sharpener |
| Christmas Tree Crate | Shed 1 Doors | Brad Nailer Box |
| Christmas Tree Ornament | Shed 2 Doors | Tripod Tablet Holder |
| Diamond Oval Picture Frame |
But after thinking about it for the last few years, I'm beginning to realize that the woodworking craze was kind of a side interest. What I really want to do is build cool mechanisms. Robots, controllers, devices for making things work. Even a Rube Goldberg. You know, where the little ball goes down the track and causes all kinds of things to happen. I just like things that work. I'm not too much into the artistic side of things, except for the tenet that form follows function. To me, if something works, works well, and makes efficient use of time and materials (and isn't covered with goop! (unless, of course goop is required for it to function)), then it's beautiful. I love flowers. They're highly efficient and functional.
Toothpick Structures
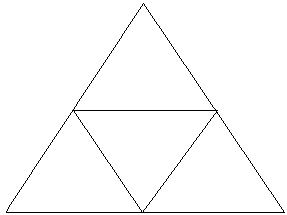
I want to talk for a moment about my toothpick structures. When I was in grade 8, the end of each chapter in my math book had a bonus question. One day I reached the bonus question, and it had a picture of a triangle filled in with little triangles, like this:

Well, the picture in the book had I don't know how many segments on each side. The bonus question was, "How many triangles are there in this picture?" In the one above, the answer is 5. So I thought about these things for awhile and decided to build the same thing in 3D instead of 2D, using toothpicks. The 3D equivalent of a triangle is a tetrahedron, and after a week or so I had one with five or six segments per side. It was actually displayed in a local art exhibition that year. Later I started to build a scale model of our house but never finished it. Maybe someday, but more likely I'll make a 3D virtual house in the computer. It's harder to crush.
But I enjoyed building the tetrahedron so much, that when I got to university I started building other polyhedra, like the icosehedron displayed on David's web page, and so on. During my third year I got kinda sick and wasn't really able to study. So I brainlessly built these structures (after doing the little bit of math it took to figure out the angles), and put them together as a mobile. To the best of my knowledge it's still hanging in the office of the head of the math department at Acadia. (If you see it, send me e-mail, please.) Eventually my doctor sent me home to recover, and after six weeks of gluing another toothpick or two between rests (i.e. during TV commercials) I finished the larger of the two structures shown here, an order 10 tetrahedron, containing 1320 toothpicks. I was proud to hang it in my dorm room (the only good thing I accomplished that year, as one of my professors described it), and after spending about twenty years in my parents' house in Truro, it was partially smashed in a car accident when my brother decided it needed to be with me instead. I have repaired it, and now it hangs by a thread in a corner of my living room. J )



The number of toothpicks in an order n tetrahedron is T(n) = n(n+1)(n+2)
So the number of toothpicks in my order 10 tetrahedron is 10 ´ 11 ´ 12 = 1320
When I get a chance I'll put the derivation of the formula here.
Meanwhile, here's a picture of an icosehedron I made. It's actually just one member of the mobile I built.